On PCA
Introduction to PCA
Principal Component Analysis (PCA), also called Empirical Orthogonal Function analysis (EOF).
Types of PCA in Biology
- For
Quantitative traits - In
Population/Micro EvolutionStudy - In
Macro EvolutionStudy
Population Case
PCA in smartpca from EIGENSOFT:
For individuals from population \(l\) with population allele frequency \(p_l\), control individuals were assigned genotype 0, 1 or 2 with probabilities \((1 - p_l)^2, 2p_l(1 - p_l)\), or \(p_l^2\), respectively.
Price, A. L., Patterson, N. J., Plenge, R. M., Weinblatt, M. E., Shadick, N. A., & Reich, D. (2006). Principal components analysis corrects for stratification in genome-wide association studies. Nature Genetics, 38(8), 904–9. doi:10.1038/ng1847
EIGENSTRAT use 0,2 for two homozygous alleles and 1 for heterozygous sites.
The EIGENSOFT package combines functionality from our population genetics methods (Patterson et al. 2006) and our EIGENSTRAT stratification correction method (Price et al. 2006). The EIGENSTRAT method uses principal components analysis to explicitly model ancestry differences between cases and controls along continuous axes of variation; the resulting correction is specific to a candidate marker’s variation in frequency across ancestral populations, minimizing spurious associations while maximizing power to detect true associations. The EIGENSOFT package has a built-in plotting script and supports multiple file formats and quantitative phenotypes.
Macro Evolution Case
PCA in jalview states:
Calculating PCAs for aligned sequences
Jalview can perform PCA analysis on both proteins and nucleotide sequence alignments. In both cases, components are generated by an eigenvector decomposition of the matrix formed from the sum of substitution matrix scores at each aligned position between each pair of sequences - computed with one of the available score matrices, such as BLOSUM62, PAM250, or the simple single nucleotide substitution matrix.
Codes at [jalview.git] / src / jalview / analysis / PCA.java
Principal component Algorithms
EIG 特征值分解
Eigenvalue decomposition (EIG) of the covariance matrix.
?princomp
The calculation is done using ‘eigen’ on the correlation or covariance matrix, as determined by ‘cor’. This is done for compatibility with the S-PLUS result. A preferred method of calculation is to use ‘svd’ on ‘x’, as is done in ‘prcomp’.
SVD 奇异值分解
Singular value decomposition (SVD) of X.
?prcomp
The calculation is done by a singular value decomposition of the (centered and possibly scaled) data matrix, not by using ‘eigen’ on the covariance matrix. This is generally the preferred method for numerical accuracy.
ALS
Alternating least squares (ALS) algorithm. This algorithm finds the best rank-k approximation by factoring X into a n-by-k left factor matrix, L, and a p-by-k right factor matrix, R, where k is the number of principal components. The factorization uses an iterative method starting with random initial values.
ALS is designed to better handle missing values. It is preferable to pairwise deletion (‘Rows’,’pairwise’) and deals with missing values without listwise deletion (‘Rows’,’complete’). It can work well for data sets with a small percentage of missing data at random, but might not perform well on sparse data sets.
?homals
##Single ranks for each variable (non-linear PCA)
res <- homals(galo, active = c(rep(TRUE, 4), FALSE), sets = list(c(1,3,4),2,5))
EIG vs SVD ? SVD !
The EIG algorithm is faster than SVD when the number of observations, n, exceeds the number of variables, p, but is less accurate because the condition number of the covariance is the square of the condition number of X.
–http://www.mathworks.com/help/stats/pca.html#namevaluepairs
Why PCA of data by means of SVD of the data? – a discussion of what are the benefits of performing PCA via SVD [short answer: numerical stability].
–http://stats.stackexchange.com/questions/134282/relationship-between-svd-and-pca-how-to-use-svd-to-perform-pca
Missing Values
See PCA / EOF for data with missing values - a comparison of accuracy.
Not all Principal Component Analysis (PCA) (also called Empirical Orthogonal Function analysis, EOF) approaches are equal when it comes to dealing with a data field that contain missing values (i.e. “gappy”). The following post compares several methods by assessing the accuracy of the derived PCs to reconstruct the “true” data set, as was similarly conducted by Taylor et al. (2013).
The gappy EOF methods to be compared are:
- LSEOF - “Least-Squares Empirical Orthogonal Functions” - The traditional approach, which modifies the covariance matrix used for the EOF decomposition by the number of paired observations, and further scales the projected PCs by these same weightings (see Björnsson and Venegas 1997, von Storch and Zweiers 1999 for details). link
- RSEOF - “Recursively Subtracted Empirical Orthogonal Functions” - This approach modifies the LSEOF approach by recursively solving for the leading EOF, whose reconstructed field is then subtracted from the original field. This recursive subtraction is done until a given stopping point (i.e. number of EOFs, % remaining variance, etc.) (see Taylor et al. 2013 for details)
- DINEOF - “Data Interpolating Empirical Orthogonal Functions” - This approach gradually solves for EOFs by means of an iterative algorothm to fit EOFS to a given number of non-missing value reference points (small percentage of observations) via RMSE minimization (see Beckers and Rixen 2003 for details). link
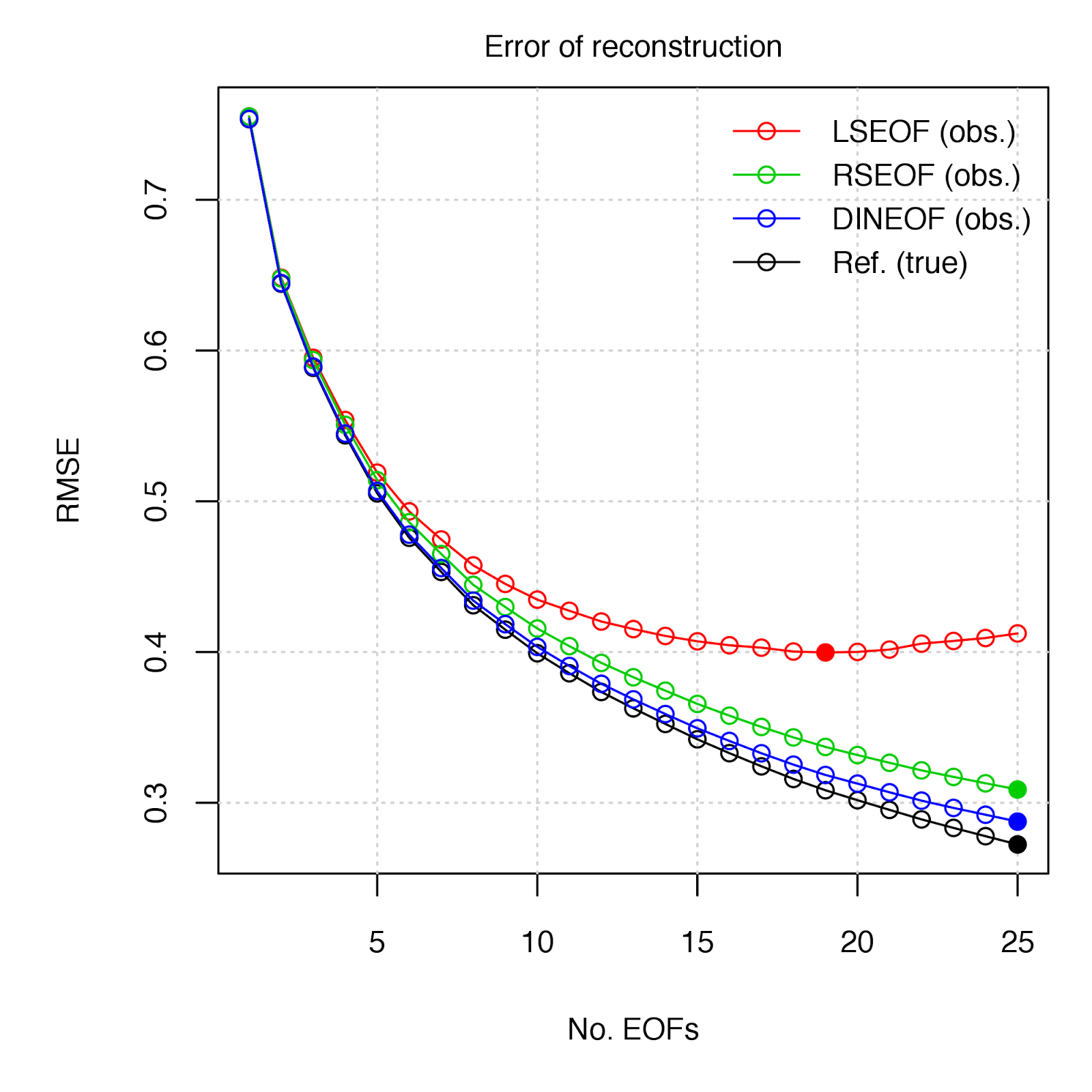
All analyses can be reproduced following installation of the “sinkr” package: https://github.com/marchtaylor/sinkr

The DINEOF method appears to be a good choice in the estimation of EOFs in gappy data. One is obviously not going to have a “true” data set by which to gauge the relative performance of approaches, but given the guidelines of selecting reference values, DINEOF should perform well under most cases. The RSEOF method also does a good job in correcting for the issues of LSEOF, and is also much less computationally intensive than DINEOF - In the SLP example, deriving 25 EOFs from the data field (dimensions = 1536 x 451) took 68 sec. with DINEOF vs 14 sec. with RSEOF (~20% of the time).
etc
- LDA和PCA
- https://liorpachter.wordpress.com/2014/05/26/what-is-principal-component-analysis/
- https://github.com/Ramlinbird/prml
- porly的博文——LDA线性判别分析
- LeftNotEasy的博文——机器学习中的数学(4):线性判别分析、主成分分析
- 攻城狮凌风——线性判别分析LDA详解
- 小林子——四大机器学习降维算法:PCA、LDA、LLE、Laplacian Eigenmaps
关于LDA,最近学习scikit_learn发现,原来存在两种推导方式——the Bayesian approach and the Fisher’s approach。两者推导过程非常不同,而且结果也存在一些差异。详情可查阅以下链接:
http://stats.stackexchange.com/questions/87975/bayesian-and-fishers-approaches-to-linear-discriminant-analysis
http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html
http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
https://liorpachter.wordpress.com/2014/05/26/what-is-principal-component-analysis/
http://www.isogg.org/wiki/Admixture_analyses
Singular value decomposition and principal component analysis (PDF)
http://stats.stackexchange.com/questions/35561/imputation-of-missing-values-for-pca
http://menugget.blogspot.com/2014/09/pca-eof-for-data-with-missing-values.html
另外,还有一个专门作PCA分析的包:pcaMethods
下面这一段来自 CRAN Task View: Chemometrics and Computational Physics http://cran.r-project.org/web/views/ChemPhys.html Principal Component Analysis
- Principal component analysis (PCA) is in the package stats as functions princomp(). Some graphical PCA representations can be found in the psy package.
- The homals package provides nonlinear PCA and, by defining sets, nonlinear canonical correlation analysis (models of the Gifi-family).
- A desired number of robust principal components can be computed with the pcaPP package. The package elasticnet is applicable to sparse PCA. The package fpca can be applied to restricted MLE for functional PCA.
- See the Multivariate task view for further packages dealing with PCA and other projection methods.
blog comments powered by Disqus

